统计学中的基本概念
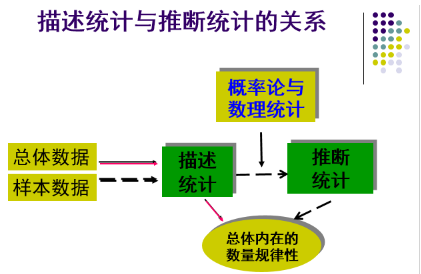
1、描述统计与推断统计
描述统计(Descriptive Statistics):用表格、图形和数字来概括、显示数据特征的统计方法。
例1:2005年我国出生人口性别比(男:女)已经升高到119.92,与正常值106相比有严重的偏离。
例2:中国经济增长的起伏
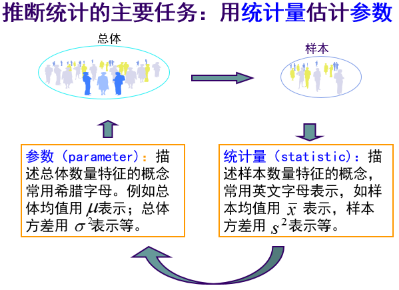
推断统计(Inferentia Statistics): 从总体中抽取样本,并利用样本数据来推断总体特征的统计方法。
总体(popuation):由统计研究所涉及的那些同质个体(也称单位)所形成的集合。
样本(sampe):所研究总体的一部分。
例1: 2003年人口变动抽样调查以全国为总体,在全国抽取了990个县(市、区)、3734个乡(镇、街道)、6544个调查小区的126万人。根据调查结果推算,2003年末全国总人口为129227万人,出生人口为1599万人,死亡人口为825万人,净增人口为774万人。
例2:一家大公司的会计部门会从所有的发票中选择一部分来检查公司所有发票的准确性。
2、数据和变量类型
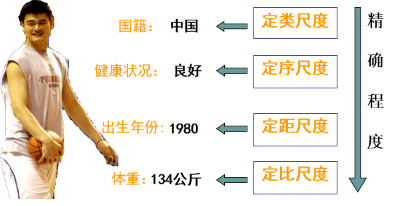
(1)、定类尺度 (Nomina Scae)
也称列名尺度、名义尺度、分类尺度
例如:性别、民族、职业
数据表现为“类别”
各类之间无等级次序
各类别可以用数字代码表示
根据定类尺度得到的数据为分类数据。
(2)、定序尺度(Ordina Scae)
也称顺序尺度
例如健康状况、质量等级
数据表现为“类别”
可对等级、大小等排序
未测量出类别之间的准确差值
根据定序尺度得到的数据为顺序数据。
(3)、定距尺度 Interva Scae
也称间隔尺度
例如年份、摄氏温度
数据表现为“数值”
可以进行加减运算
“0”是只是尺度上的一个点,不代表“不存在”
根据定距尺度得到的数据为间距数据。
(4)、定比尺度 Ratio Scae
也称比率尺度
例如体重、身高
数据表现为“数值”
可以进行加减、乘除运算
“0”表示“没有”或“不存在”
根据定比尺度得到的数据为比率数据。
定距尺度与定比尺度的区别
定距尺度中“0”表示一个具体数值,不表示“没有”或“不存在”,定比尺度中“0”表示“没有”或“不存在” 。
在实际应用中定距尺度与定比尺度差别微不足道,往往不作区分。 例如在SPSS Statistics软件中,数据的计量尺度被分为3类:名义(Nomina)、有序(Ordina)、 度量(Scae )
四种计量尺度的比较
1、四种尺度所包含的信息量是依次递增的,级别由低到高。
2、根据较高层次的计量尺度可以获得较低层次的计量尺度。
3、不同的尺度数据对应这不同数据显示方法和分析方法。
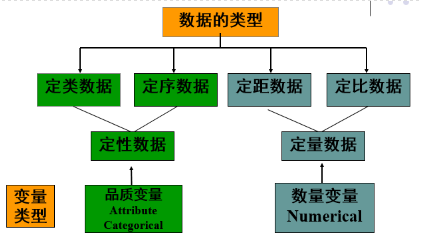
数据和变量类型:总结
变量的概念和类型
变量是用来描述现象某种令人感兴趣的特征的概念。
品质变量是描述个体有关属性特征的变量,本质上不能用数字来表示。例如性别。
数量变量是描述个体有关数量特征的变量,都是用数字来表示的。例如人数,年龄等。
离散型变量指的是有限个数值或诸如0,1,2……之类无限可列值的变量。
如果某一变量可以取某一区间或多个区间中任意数值,则该变量称为连续型变量。
横截面、时间序列和面板数据
横截面数据(Cross-sectiona data)是在同一时点或是大约在同一时点所收集的数据。
例如2016年我国各直辖市的GDP 。
时间序列数据(Time series data)是按时间顺序取得的一系列数据。
例如我国历年的GDP。
面板数据(Pane Data):对多个事物在不同时期或时点上进行测量得到的数据 。如1996-2016年全国各个省份的GDP
3、统计指标的概念
一般有两种理解和两种使用方法:
1、统计指标是指反映现象数量特征的概念。如年末人口数、商品销售额、劳动生产率等。
2、统计指标是反映现象数量特征的概念和具体数值。如我国2016年的国内生产总值 。
(1)总量指标
也称为绝对数:以绝对数形式表现现象规模和水平的统计指标。可以分为时点数和时期数。
例如,2007全年入境旅游人数13187万人次 ;2007年全年国内生产总值246619亿元 ;2007年末全国参加城镇基本养老保险人数为20107万人 .
(2)时点数和时期数
时点数:是描述某种现象在某一个特定时刻(某一瞬间或某一时点)数量表现的数据。
例如,2007年年末全国总人口为132129万人 。
时期数:是描述某种现象在某一个特定时间范围内所实现的成果的数据。例如,2004年我国全年各种运输方式完成货物运输周转量66698亿吨公里。
区分数据是时点数还是时期数的方法之一看其加总后的结果是否有意义。若有意义则该指标必定是时期数。反之,则必定是时点数。
(3)相对数和平均数
相对指标:采用两个有联系的数值进行对比而得到的比值。也称为相对数,如产业结构比例、性别比、人口密度等等。
平均指标:也称为平均数,反映现象在某一时间或空间上的平均数量水平。例如职工的平均工资,平均考试成绩,等等。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在当今数据驱动的时代,数据分析能力备受青睐,数据分析能力频繁出现在岗位需求的描述中,不分岗位的任职要求中,会特意标出“熟 ...
2025-04-03在当今数字化时代,数据分析师的重要性与日俱增。但许多人在踏上这条职业道路时,往往充满疑惑: 如何成为一名数据分析师?成为 ...
2025-04-02最近我发现一个绝招,用DeepSeek AI处理Excel数据简直太爽了!处理速度嘎嘎快! 平常一整天的表格处理工作,现在只要三步就能搞 ...
2025-04-01你是否被统计学复杂的理论和晦涩的公式劝退过?别担心,“山有木兮:统计学极简入门(Python)” 将为你一一化解这些难题。课程 ...
2025-03-31在电商、零售、甚至内容付费业务中,你真的了解你的客户吗? 有些客户下了一两次单就消失了,有些人每个月都回购,有些人曾经是 ...
2025-03-31在数字化浪潮中,数据驱动决策已成为企业发展的核心竞争力,数据分析人才的需求持续飙升。世界经济论坛发布的《未来就业报告》, ...
2025-03-28你有没有遇到过这样的情况?流量进来了,转化率却不高,辛辛苦苦拉来的用户,最后大部分都悄无声息地离开了,这时候漏斗分析就非 ...
2025-03-27TensorFlow Datasets(TFDS)是一个用于下载、管理和预处理机器学习数据集的库。它提供了易于使用的API,允许用户从现有集合中 ...
2025-03-26"不谋全局者,不足谋一域。"在数据驱动的商业时代,战略级数据分析能力已成为职场核心竞争力。《CDA二级教材:商业策略数据分析 ...
2025-03-26当你在某宝刷到【猜你喜欢】时,当抖音精准推来你的梦中情猫时,当美团外卖弹窗刚好是你想吃的火锅店…… 恭喜你,你正在被用户 ...
2025-03-26当面试官问起随机森林时,他到底在考察什么? ""请解释随机森林的原理""——这是数据分析岗位面试中的经典问题。但你可能不知道 ...
2025-03-25在数字化浪潮席卷的当下,数据俨然成为企业的命脉,贯穿于业务运作的各个环节。从线上到线下,从平台的交易数据,到门店的运营 ...
2025-03-25在互联网和移动应用领域,DAU(日活跃用户数)是一个耳熟能详的指标。无论是产品经理、运营,还是数据分析师,DAU都是衡量产品 ...
2025-03-24ABtest做的好,产品优化效果差不了!可见ABtest在评估优化策略的效果方面地位还是很高的,那么如何在业务中应用ABtest? 结合企业 ...
2025-03-21在企业数据分析中,指标体系是至关重要的工具。不仅帮助企业统一数据标准、提升数据质量,还能为业务决策提供有力支持。本文将围 ...
2025-03-20解锁数据分析师高薪密码,CDA 脱产就业班助你逆袭! 在数字化浪潮中,数据驱动决策已成为企业发展的核心竞争力,数据分析人才的 ...
2025-03-19在 MySQL 数据库中,查询一张表但是不包含某个字段可以通过以下两种方法实现:使用 SELECT 子句以明确指定想要的字段,或者使 ...
2025-03-17在当今数字化时代,数据成为企业发展的关键驱动力,而用户画像作为数据分析的重要成果,改变了企业理解用户、开展业务的方式。无 ...
2025-03-172025年是智能体(AI Agent)的元年,大模型和智能体的发展比较迅猛。感觉年初的deepseek刚火没多久,这几天Manus又成为媒体头条 ...
2025-03-14以下的文章内容来源于柯家媛老师的专栏,如果您想阅读专栏《小白必备的数据思维课》,点击下方链接 https://edu.cda.cn/goods/sh ...
2025-03-13